고정 헤더 영역
상세 컨텐츠
본문
3.6 부동소수점 표현 (Floating - point representation) :
소수점의 위치를 이동시킬 수 있는 수 표현 방법 -> 수 표현 범위 확대
부동소수점 수 (floating - point number)의 일반적인 형태

10진 부동소수점 수(decimal floating - point number)

2진 부동소수점 수 (binary floating - point number)

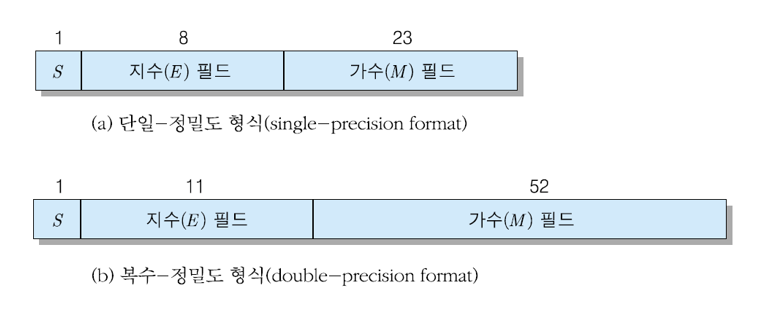
- 단일-정밀도(single-precision) 부동소수점 수 : 32비트
- 복수-정밀도(double-precision) 부동소수점 수 : 64비트

같은 수에 대한 부동소수점 표현이 여러 가지 존재

정규화된 표현(Normalized representation) :
수에 대한 표현을 한 가지로 통일하기 위한 방법


※ 소수점 아래 첫 번째 비트는 항상 1이므로, 반드시 저장할 필요는 없음
-> 가수 23비트를 활용하여 소수점 아래 24자리 수 까지 표현 가능
바이어스된 지수 (biased exponent) :
지수를 바이어스된 수 (biased number)로 표현 (일정 수를 더함)
사용 목적
- 0(혹은 0에 매우 가까운 값)에 대한 표현에서 모든 비트들이 0이 되도록 함으로써, 0-검사가 용이하게 하기 위함
-> 0-검사가 정수 경우와 같은 방법으로 가능해짐


부동소수점 수의 표현 범위

IEEE 754 표준 부동소수점 수의 형식
부동소수점 수의 표현 방식의 통일을 위하여 미국전기전자공학회(IEEE)에서 정의한 표준
32-비트 단일-정밀도 부동소수점 수의 표현

- 가수 : 부호화-크기 표현 사용
- 지수 필드 : 바이어스 127 사용
- 소수점 아래의 M 부분만 가수 필드에 저장 (소수점 왼쪽의 저장되지 않는 1을 hidden bit라고 함)
64-비트 복수-정밀도 부동소수점 수의 표현

- 지수필드 : 바이어스1023 사용

예외 경우를 포함한 정의 (32비트 형식) - 참고

예외 경우를 포함한 정의 (64비트 형식)

4배수-정밀도(quadruple-precision : 128 비트) 부동소수점 수의 표현

- 가수 : 부호화-크기 표현 사용
- 지수 필드 : 바이서스 16383 사용 (범위 : -16382 ~ +16383)

3.7 부동소수점 산술 연산
3.7.1 덧셈과 뺄셈
- 지수들이 일치되도록 조정 (alignment)
- 가수들 간의 연산(더하기 혹은 빼기) 수행
- 결과를 정규화 (normalization)


부동소수점 산술의 파이프라이닝
- 연산 과정을 독립적 단계들로 분리 가능
- 단계 수 만큼의 속도 향상
- 대규모의 부동소수점 계산을 처리하는 거의 모든 슈퍼컴퓨터들에서 채택
C(I) = A(I) + B(I)

3.7.2 부동소수점 곱셈/나눗셈
2진수 부동소수점 곱셈 과정
- 가수들을 곱한다
- 지수들을 더한다
- 결과값을 정규화

2진수 부동소수점 나눗셈 과정
- 가수들을 나눈다
- 피제수의 지수에서 제수의 지수를 뺀다
- 결과값을 정규화
부동소수점 연산 과정에서 발생 가능한 문제점
1. 지수 오버플로우 (exponent overflow)
- 양의 지수값이 최대 지수값을 초과 (수가 너무 커서 표현될 수 없는 상태이므로, +∞또는 -∞로 세트)
2. 지수 언더플로우 (exponent underflow)
- 음의 지수값이 최대 지수값을 초과 (수가 너무 작아서 표현될 수 없는 상태이므로, 0으로 세트)
3. 가수 언더플로우 (mantissa underflow)
- 가수의 소수점 위치 조정 과정에서 비트들이 가수의 우측 편으로 넘치는 상태 (반올림 적용)
4. 가수 오버플로우 (mantissa overflow)
- 같은 부호를 가진 두 가수들을 덧셈하였을 때 올림수가 발생 (재조정 과정을 통하여 정규화)
'Computer Science > Computer Architecture' 카테고리의 다른 글
| 04. 제어 유니트 (2) [마이크로 명령어의 형식] (0) | 2020.04.22 |
|---|---|
| 04. 제어 유니트 (1) [제어 유니트의 기능/구조] (0) | 2020.04.22 |
| 03. 컴퓨터 산술과 논리 연산 (3) [정수의 산술 연산] (0) | 2020.04.08 |
| 03. 컴퓨터 산술과 논리 연산(2) [논리 연산, 시프트 연산] (0) | 2020.04.08 |
| 03. 컴퓨터 산술과 논리 연산 (1) [ALU의 구성 요소, 정수의 표현] (0) | 2020.04.08 |





댓글 영역